Т.к. уж что-что, а в математику я умею получше многих, то это прозвучало для меня обидно, а потому вот вам простой пример. Итак, вы берёте у банка кредит на 100 000 рублей (сто тысяч рублей) на один год (12 месяца) под 20 процентов годовых. Внимание вопрос — рассчитайте в уме (или на бумажке) — сколько будет итоговая сумма переплаты и сколько будет составлять ежемесячный платёж? Для простоты будем считать ежемесячный платёж постоянным (это называется аннуитетный вид платежа).
Итак, сколько? Если вы насчитали 20 000 рублей переплаты — поздравляю, вы насчитали неверно и понимаете в схеме работы банковских кредитов не больше моего (я бы рассчитал также — это ведь весьма очевидно). Если вы «прикинули приблизительно» — поздравляю, вы вообще провалили это простое задание — никто не платит «приблизительно», да и математика — она вообще точная наука, а не приблизительная.
В общем, если вы сдаётесь, то вот вам расчёт по кредитному калькулятору:
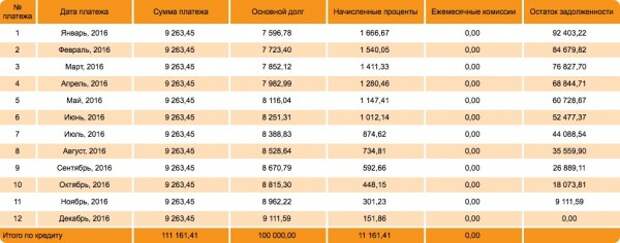
Итак, переплата в нашем случае составит 11 161,41 рубль, а ежемесячный платёж — 9263,45 рублей. Как эти цифры получить? Ну, прежде всего, вам нужно как раз забыть ту математику, которой вас учили в школе (математику здорового человека) ибо все кредиты банки рассчитывают по математике курильщика.
Вот вы взяли 100 000 рублей. А потом в первый же месяц что-то выплатили. Сумма вашего долга уменьшилась — а потому дальше согласно тому самому проценту наценка будет уже меньше т.к. будет каждый месяц рассчитываться из остатка долга, а не из всей суммы долга. Понятно? Допустим. А теперь внимание вопрос: почему же ставка по кредиту называется годовым процентом, если сумма по ней меняется каждый месяц? Потому, что это математика курильщика.
Далее. При одинаковых условиях, но при разном виде платежа (аннуитетный — когда ежемесячный платёж постоянный и дифференцированный — когда он постепенно уменьшается) вы заплатите разное количество денег. При аннуитетном, как мы уже выяснили, вы заплатите банку 111 161,41 рубль, а при дифференцированном — 110 833,33 рубля. Почему при одинаковой ставке и сумме кредита сумма выплат разная? Потому, что математика курильщика. Впрочем, вы теперь знаете, что дифференцированный платёж выгоднее — в итоге заплатите меньше и каждый месяц будете платить всё меньше (как-то мотивирует, что ли).
С одной стороны — ну круто же, общая сумма выплат меньше, чем рассчитанная по математике здорового человека. С другой — очевидно, что суть расчёта ускользает
от здравого смысла, и это просто вопрос времени — где конкретно эта математика курильщика начнёт работать против вас, ведь она придумана именно для того, чтобы работать против вас. Самое главное — что чем дольше срок кредита, тем больше вы переплачиваете (и не подумайте, что если увеличить срок кредита в два раза, то и переплата увеличится в два раза — вовсе нет, хотя примерно). А сбоить эта математика начнёт, если вы решите выплачивать не строго по схеме, а «заранее» или с опозданием.
Кстати, в некоторых случаях (вроде как это прописывают в договоре), банк может и изменить процентную ставку по кретиду. Т.е. все эти ваши расчёты даже по кредитному калькулятору надо будет пересчитывать. И как — это отдельный вопрос, ибо часть долга-то вы уже вернули.
Ну и главный вопрос: что нужно знать нормальному человеку, когда он берёт кредит и чего ему некоторые банки не скажут вообще, а другие — нехотя и из-под палки? Ему нужно знать следующее: «Если вы возьмёте у нас в кредит сто тысяч рублей на один год с постоянным ежемесячным платежом, то в общей сложности должны будете вернуть нам 111 161,41 рубль, таким образом ставка по кредиту для вашего случая составит примерно 11 процентов». Вот и всё. Это — математика здорового человека.
P.S. Кстати, если приглядитесь, на первом скриншоте есть уточнение, что в каждом банке могут быть свои особенности расчётов. Так что, имейте ввиду, что математика курильщика у каждого банка — своя.
